Stress tensor

Cauchy formula in 2D

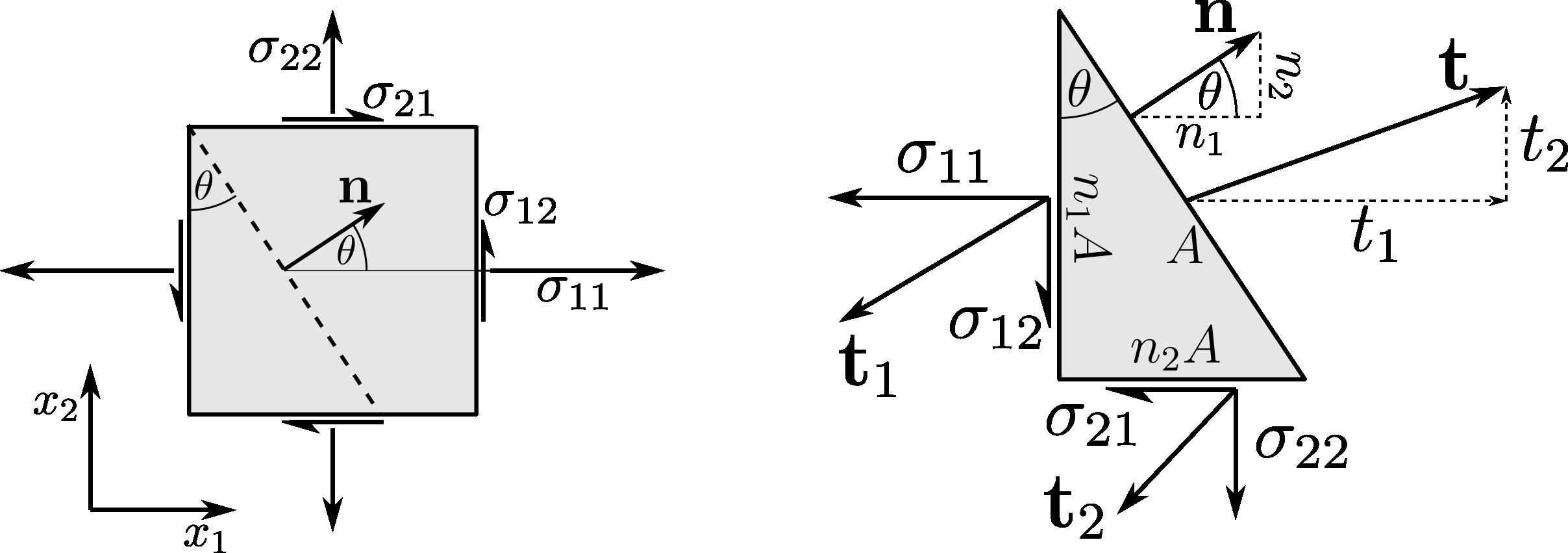
The equilibrium of forces, i.e. Euler’s first law of motion (Newton’s second law of motion) for 2D triangle:

\[\mathbf{t}A = \mathbf{t}_1 A_1 + \mathbf{t}_2 A_2\]

The area of the faces of the triangle perpendicular to the axes can be found by projecting \(A\) into each face

\[\mathbf{t}A = \mathbf{t}_1 n_1 A + \mathbf{t}_2 n_2 A\]

than divided by \(A\) gives:

\[\mathbf{t} = \mathbf{t}_1 n_1 + \mathbf{t}_2 n_2\]

This equation could be written by components

\[\begin{split}\begin{aligned} t_1 &= \sigma_{11} n_1 + \sigma_{21} n_2 \\ t_2 &= \sigma_{12} n_1 + \sigma_{22} n_2 \end{aligned}\end{split}\]

or in matrix form

\[\begin{split}\begin{bmatrix}t_1\\t_2\end{bmatrix}= \begin{bmatrix} \sigma_{11} & \sigma_{21}\\ \sigma_{12} & \sigma_{22} \end{bmatrix} \cdot \begin{bmatrix} n_1\\ n_2 \end{bmatrix} \quad \text{or} \quad \mathbf{t} = \boldsymbol{\sigma} \cdot \mathbf{n} \quad \text{where} \quad \boldsymbol{\sigma} = \begin{bmatrix}\mathbf{t}_1 & \mathbf{t}_2\end{bmatrix}\end{split}\]

Because the \(\sigma_{12} = \sigma_{21}\) (conservation of angular momentum), the \(\boldsymbol{\sigma}\) must be symmetric.

Matrix as function

Note that \(\boldsymbol{\sigma}\), known as stress tensor operates as a function, i.e. each normal unit vector \(\mathbf{n}\) is transformed to traction vector \(\mathbf{t}\) acting on the plane normal to \(\mathbf{n}\). In this way, stress tensor describing stress on arbitrary plane, i.e describing stress in point.

S = stress2([[-8,  2],
             [ 2, -5]])
n = vec2(60)  # unit length vector oriented 60 degrees from x
S.cauchy(n)  # traction vector

Vector2(-2.268, -3.33)

Cauchy formula in 3D

The tetrahedron is formed by slicing the infinitesimal element along an arbitrary plane with normal \(\mathbf{n}\). The traction vector on this plane is denoted by \(\mathbf{t}\). The traction vectors acting on the faces of the tetrahedron are denoted as \(\mathbf{t}_1\), \(\mathbf{t}_2\), and \(\mathbf{t}_3\), and are by definition the components of the stress tensor \(\boldsymbol{\sigma}\).

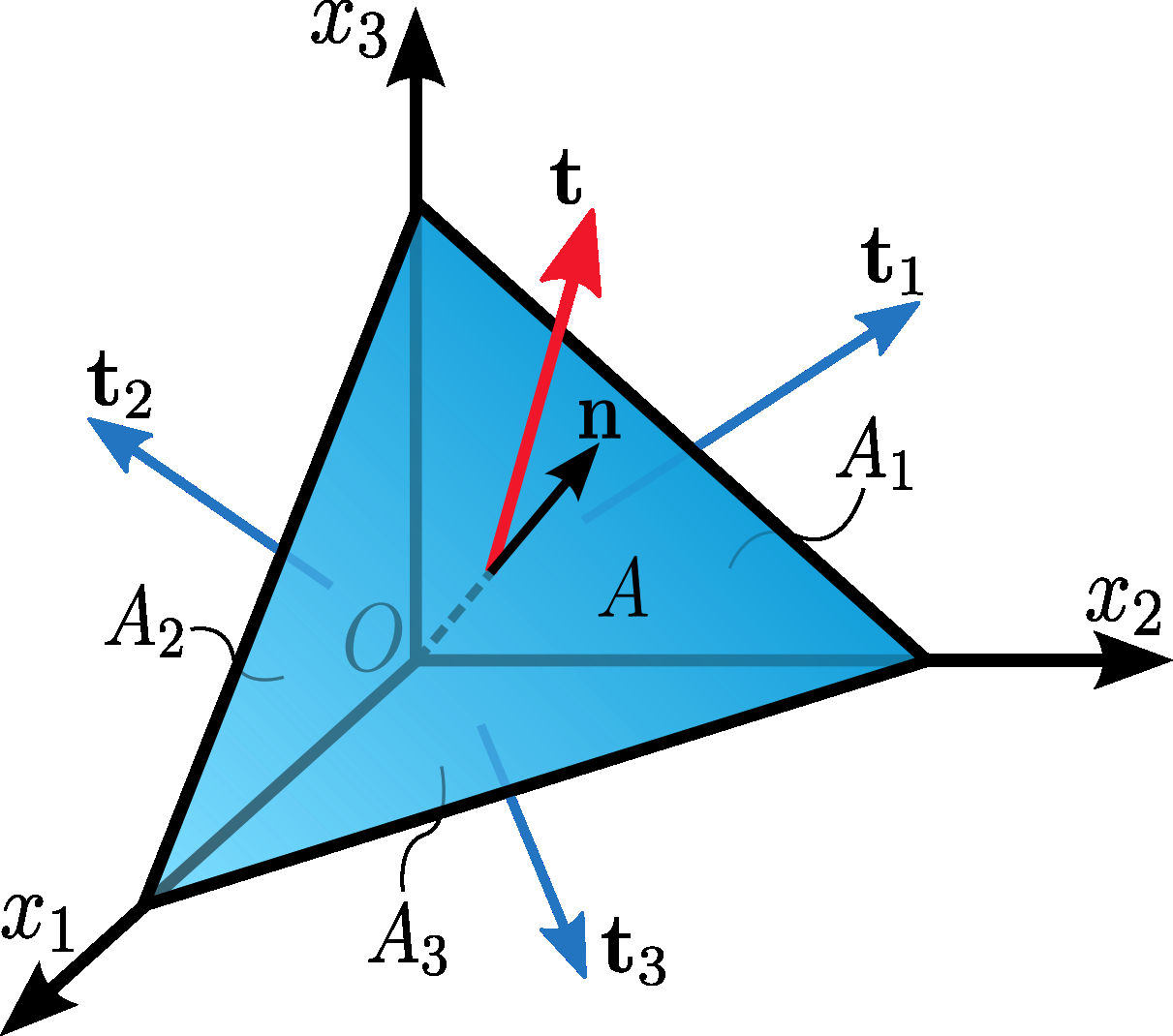
Similarly to 2D case, the equilibrium of forces, i.e. Euler’s first law of motion (Newton’s second law of motion), gives:

\[\mathbf{t} A = \mathbf{t}_1 A_1 + \mathbf{t}_2 A_2 + \mathbf{t}_3 A_3\]

The area of the faces of the tetrahedron perpendicular to the axes can be found by projecting \(A\) into each face:

\[\mathbf{t} A = \mathbf{t}_1 n_1 A + \mathbf{t}_2 n_2 A + \mathbf{t}_3 n_3 A\]

than divided by \(A\) gives:

\[\mathbf{t} = \mathbf{t}_1 n_1 + \mathbf{t}_2 n_2 + \mathbf{t}_3 n_3\]

What is tensor

Tensors are algebraic objects that describe linear relationship between vectors, scalars, or tensors. Here, any linear connection between two physical vector quantities is called a tensor, reflecting original use to describe the “tensions” in a material.

\[\begin{split}\left[{\begin{matrix} u_1 \\ u_2 \\ u_3 \end{matrix}}\right] = \left[{\begin{matrix} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{matrix}}\right] \left[{\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix}}\right]\end{split}\]

\[\mathbf{u} = \mathbf{A} \cdot \mathbf{v}\]

Cauchy stress tensor

In continuum mechanics, the Cauchy stress tensor \(\boldsymbol{\sigma}\) is a second order tensor, with nine components \(\sigma_{ij}\), that completely define the state of stress at a point inside a material.

According to the principle of conservation of angular momentum, equilibrium requires that the summation of moments with respect to an arbitrary point is zero, which leads to the conclusion that the stress tensor is symmetric, thus having only six independent stress components, instead of the original nine.

\[\begin{split}\boldsymbol{\sigma} = \sigma_{ij} = \left[{\begin{matrix} \mathbf{t}_1 & \mathbf{t}_2 & \mathbf{t}_3 \end{matrix}}\right] = \left[{\begin{matrix} \sigma _{11} & \sigma _{21} & \sigma _{31} \\ \sigma _{12} & \sigma _{22} & \sigma _{32} \\ \sigma _{13} & \sigma _{23} & \sigma _{33} \end{matrix}}\right]\end{split}\]

\[\begin{split}\left[{\begin{matrix} \sigma _{11} & \sigma _{21} & \sigma _{31} \\ \sigma _{12} & \sigma _{22} & \sigma _{32} \\ \sigma _{13} & \sigma _{23} & \sigma _{33} \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _{xx} & \sigma _{yx} & \sigma _{zx} \\ \sigma _{xy} & \sigma _{yy} & \sigma _{zy} \\ \sigma _{xz} & \sigma _{yz} & \sigma _{zz} \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _x & \tau _{xy} & \tau _{xz} \\ \tau _{xy} & \sigma _y & \tau _{yz} \\ \tau _{xz} & \tau _{yz} & \sigma _z \\ \end{matrix}}\right]\end{split}\]

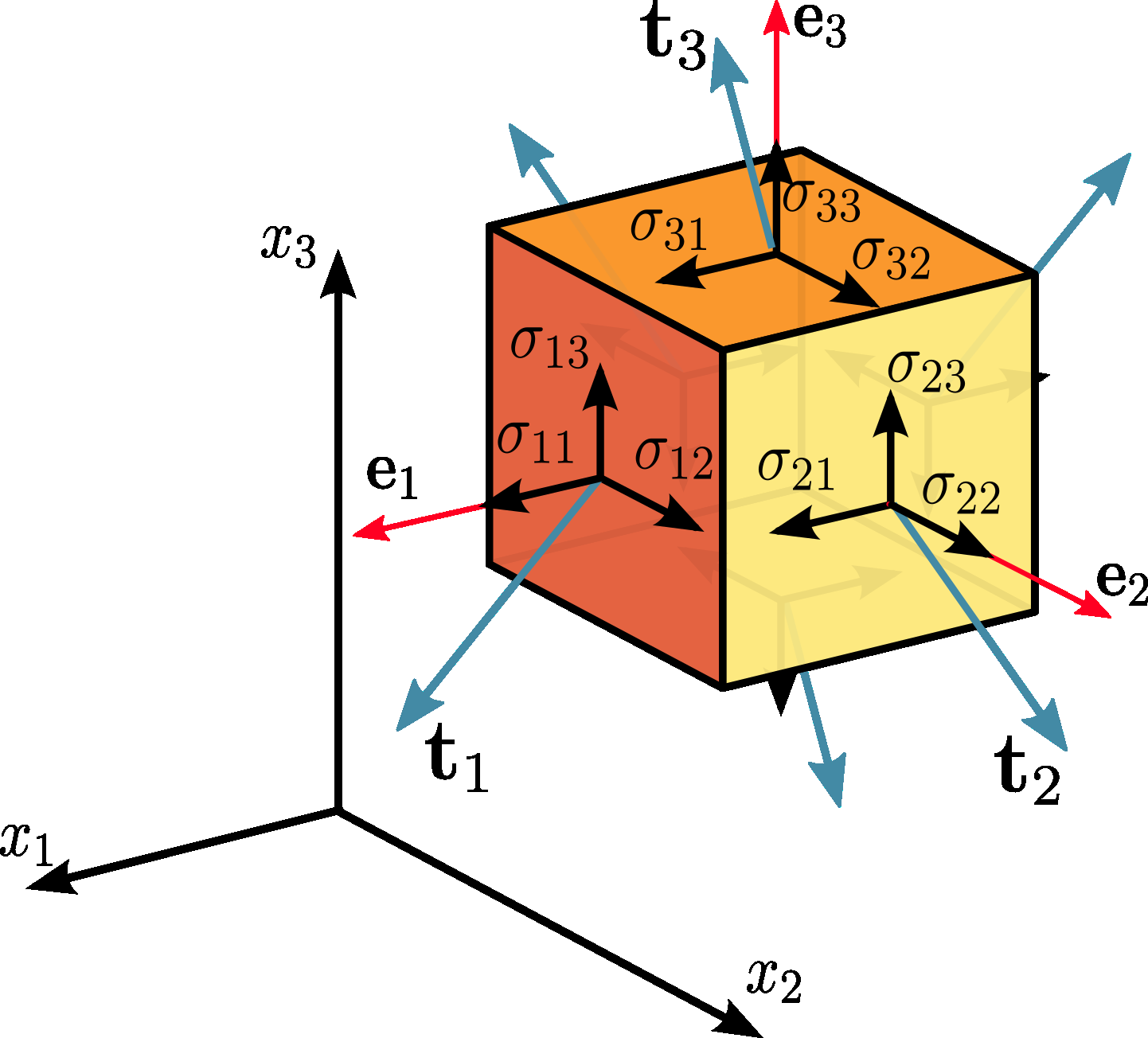
where \(\sigma_{11}\), \(\sigma_{22}\), \(\sigma_{33}\) are normal stresses, and \(\sigma_{12}\), \(\sigma_{13}\), \(\sigma_{21}\), \(\sigma_{23}\), \(\sigma_{31}\), \(\sigma_{32}\) are shear stresses.

Indexes of stress components

The first index \(i\) indicates that the stress acts on a plane normal to the \(x_i\)-axis, and the second index \(j\) denotes the direction in which the stress acts.

Cauchy’s stress theorem

According to Cauchy’s fundamental theorem, also called Cauchy’s stress theorem, merely by knowing the traction vectors on three mutually perpendicular planes, the stress vector on any other plane passing through that point can be found using transformation equation.

\[\begin{split}\mathbf{t} \equiv \left[{\begin{matrix} \mathbf{t}_1 & \mathbf{t}_2 & \mathbf{t}_3 \end{matrix}}\right] = \left[{\begin{matrix} \sigma _{11} & \sigma _{21} & \sigma _{31} \\ \sigma _{12} & \sigma _{22} & \sigma _{32} \\ \sigma _{13} & \sigma _{23} & \sigma _{33} \end{matrix}}\right] \cdot \left[{\begin{matrix} n_1 \\ n_2 \\ n_3 \end{matrix}}\right] \quad \text{or} \quad \mathbf{t} = \boldsymbol{\sigma} \cdot \mathbf{n}\end{split}\]

This equation implies that the traction vector \(\mathbf{t}\) at any point \(P\) in a continuum associated with a plane given by unit normal vector \(\mathbf{n}\), can be expressed as a function of the traction vectors on the planes perpendicular to the coordinate axes, i.e. stress tensor \(\boldsymbol{\sigma}\).

S = stress.from_comp(xx=-8, yy=-6, zz=-2)
S

Stress3
[[-8  0  0]
 [ 0 -6  0]
 [ 0  0 -2]]

n = fol(150, 60)  # normal of plane
t = S.cauchy(n)  # traction vector
print(f'Magnitude of normal stress on plane {n} is {abs(t.project(n))}')
print(f'Magnitude of shear stress on plane {n} is {abs(t.reject(n))}')

Magnitude of normal stress on plane S:150/60 is 6.125
Magnitude of shear stress on plane S:150/60 is 2.496873044429773

In APSG you can use the stress_comp method of the stress tensor:

sn, tau = S.stress_comp(n)
print(f'Magnitude of normal stress on plane {n} is {abs(sn)}')
print(f'Magnitude of shear stress on plane {n} is {abs(tau)}')

Magnitude of normal stress on plane S:150/60 is 6.125
Magnitude of shear stress on plane S:150/60 is 2.496873044429773

Sign convention

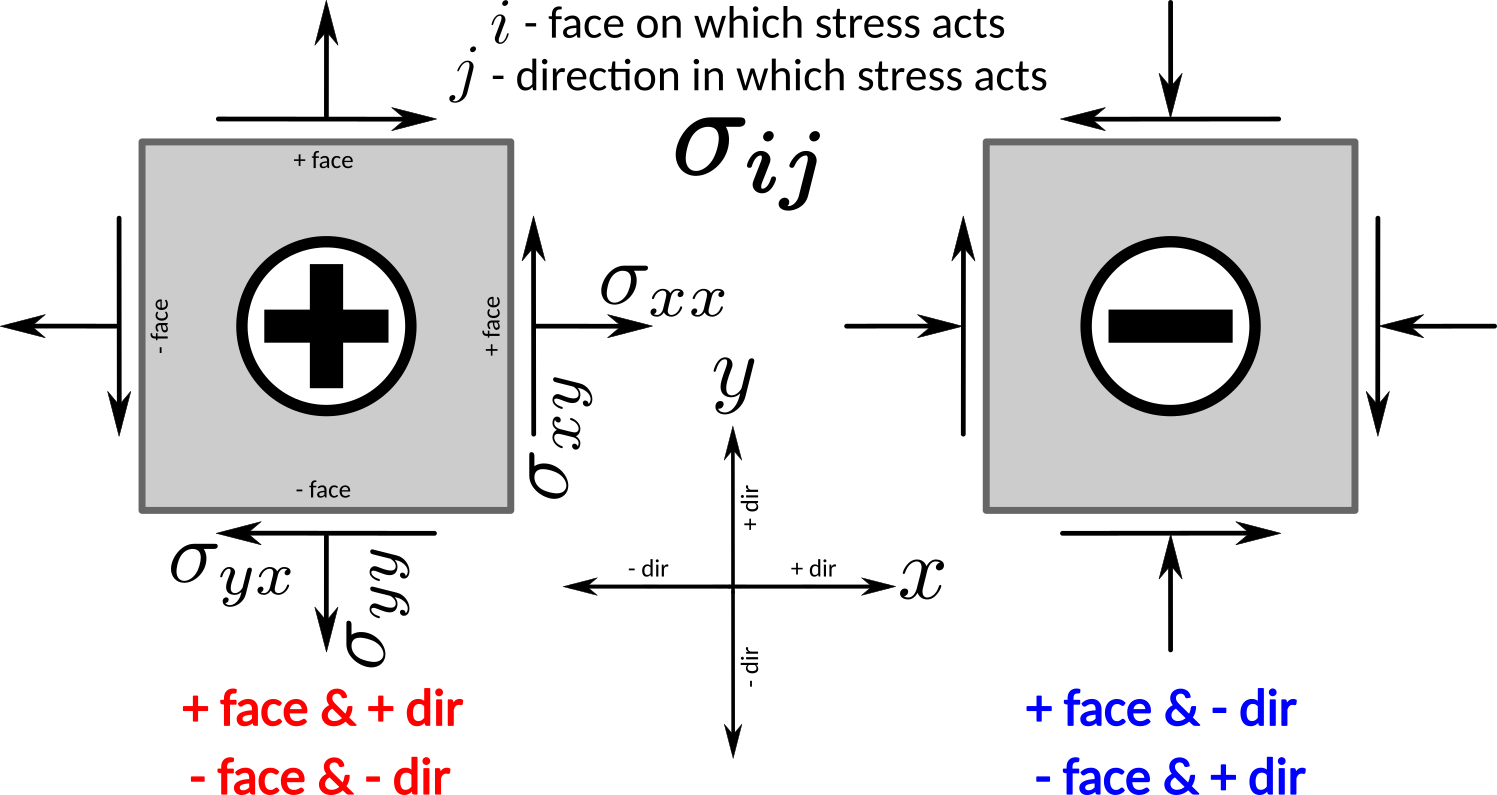
Sign convention for stress components

A stress component is positive if it acts in the positive direction of the coordinate axes, and if the plane where it acts has an outward normal vector pointing in the positive coordinate direction.