Introduction to kinematic analysis

Deformation is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, body forces (such as gravity), or changes in temperature, pressure, or chemical reactions, etc.

Strain is related to deformation in terms of relative displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body. Here we will follow simplified view.

In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The relation between stress and strain is expressed by constitutive equations, e.g., Hooke’s law for linear elastic materials. Deformations which cease to exist after the stress field is removed are termed as elastic deformation. In this case, the continuum completely recovers its original configuration. On the other hand, irreversible deformations remain. They exist even after stresses have been removed. One type of irreversible deformation is plastic deformation, which occurs in material bodies after stresses have attained a certain threshold value known as the elastic limit or yield stress, and are the result of slip, or dislocation mechanisms at the atomic level. Another type of irreversible deformation is viscous deformation, which is the irreversible part of viscoelastic deformation.

Components of deformation

A change in the configuration of a continuum body results in a displacement from an \textbf{initial or undeformed configuration} to a current or \textbf{deformed configuration}.

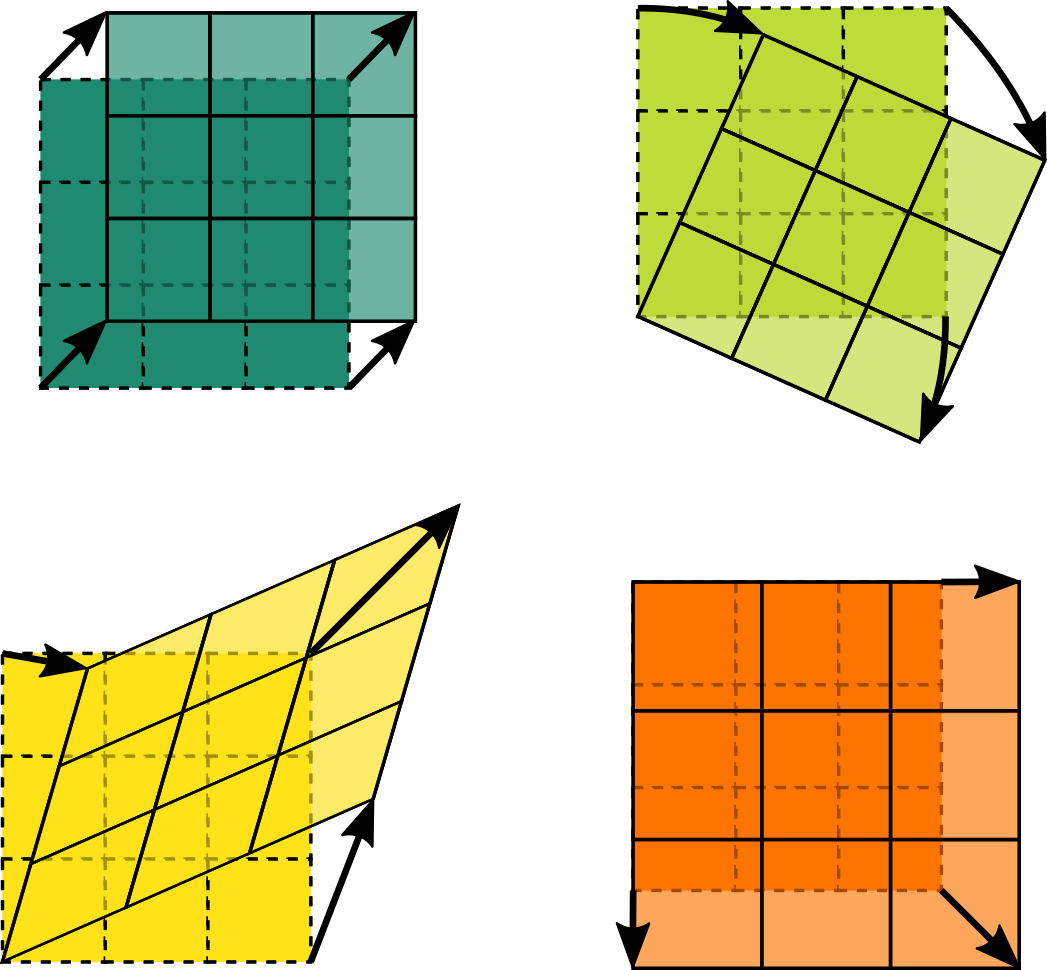
The displacement of a body has two components:

• Rigid-body displacement implies no relative displacement of particles in the body, i.e. there is no change in shape and size of the body from an initial or undeformed configuration

  • Translation

  • Rotation

• Deformation or strain implies relative displacement of particles in the body, i.e. the change in shape and/or size of the body from an initial or undeformed configuration

  • Distortion - isochoric change in shape

  • Dilation - change in volume

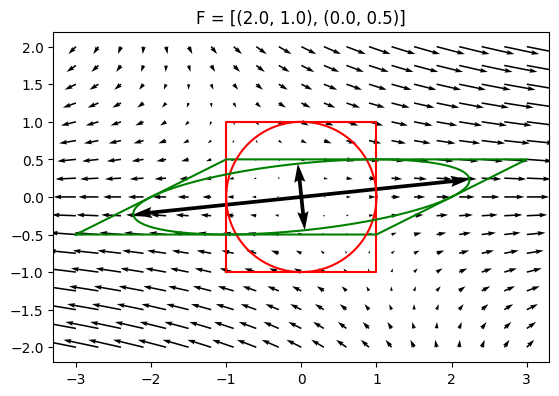
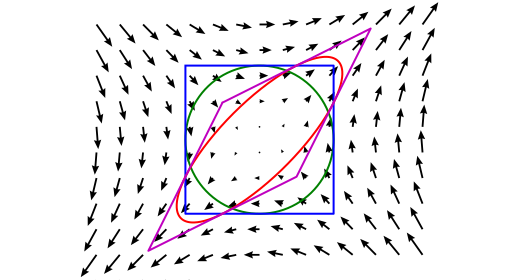
Homogeneous deformation

A deformation is called an homogeneous (also called affine deformation) if it can be described by an affine transformation. Such a transformation is composed of a linear transformation (such as rotation, shear, extension and compression) and a rigid body translation. Every part of the material deforms as the whole does, and straight parallel lines in the reference configuration map to straight parallel lines in the deformed configuration.

\[\begin{split}\begin{aligned}x &= aX+bY+t_X \\ y &= cX+dY+t_Y \end{aligned}\end{split}\]

or in matrix form:

\[\begin{split}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix}X \\ Y \end{bmatrix} + \begin{bmatrix} t_X \\ t_Y \end{bmatrix}\end{split}\]

Note

Properties of homogeneous deformation are not spatially dependent.

Deformation gradient

Without translation the homogeneous deformation (rotation and strain) could be described as:

\[\begin{split}\begin{aligned}x &= aX+bY \\ y &= cX+dY \end{aligned}\end{split}\]

\[\begin{split} \begin{bmatrix}x \\ y\end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix}X \\ Y\end{bmatrix}\end{split}\]

or

\[\mathbf{x}=\boldsymbol{F}\mathbf{X}\]

where \(\boldsymbol{F}\) is so called deformation gradient.

Note, that as we excluded translation, the origin of coordinates do not change during deformation:

\[\begin{split}\begin{bmatrix} 0 \\ 0 \end{bmatrix}=\boldsymbol{F}\begin{bmatrix} 0 \\ 0 \end{bmatrix}\end{split}\]

Displacement gradient

Displacement of particle is vector between initial and final postion, i.e:

\[\begin{split}\begin{aligned}u &= x-X = aX+bY-X = (a-1)X+bY\\ v &= y-Y = cX+dY-Y = cX+(d-1)Y\end{aligned}\end{split}\]

\[\begin{split}\begin{bmatrix}u \\ v\end{bmatrix}=\begin{bmatrix} a-1 & b \\ c & d-1 \end{bmatrix}\begin{bmatrix}X \\ Y\end{bmatrix}\end{split}\]

or

\[\mathbf{u}=(\boldsymbol{F}-\boldsymbol{I})\mathbf{X}=(\boldsymbol{\nabla u})\mathbf{X}\]

where \(\boldsymbol{\nabla}\boldsymbol{u}\) is so called displacement gradient.

Python exercise

F = defgrad2([[2, 1],[0, 0.5]])
plot_defgrad(F)